Statistical Models for the Latent Space: From Gaussian VAE to Kuramoto-Enhanced S-VAE

Table of Links

Abstract and 1. Introduction

2. Some recent trends in theoretical ML

   2.1 Deep Learning via continuous-time controlled dynamical system

   2.2 Probabilistic modeling and inference in DL

   2.3 Deep Learning in non-Euclidean spaces

   2.4 Physics Informed ML

3. Kuramoto model

   3.1 Kuramoto models from the geometric point of view

   3.2 Hyperbolic geometry of Kuramoto ensembles

   3.3 Kuramoto models with several globally coupled sub-ensembles

4. Kuramoto models on higher-dimensional manifolds

   4.1 Non-Abelian Kuramoto models on Lie groups

   4.2 Kuramoto models on spheres

   4.3 Kuramoto models on spheres with several globally coupled sub-ensembles

   4.4 Kuramoto models as gradient flows

   4.5 Consensus algorithms on other manifolds

5. Directional statistics and swarms on manifolds for probabilistic modeling and inference on Riemannian manifolds

   5.1 Statistical models over circles and tori

   5.2 Statistical models over spheres

   5.3 Statistical models over hyperbolic spaces

   5.4 Statistical models over orthogonal groups, Grassmannians, homogeneous spaces

6. Swarms on manifolds for DL

   6.1 Training swarms on manifolds for supervised ML

   6.2 Swarms on manifolds and directional statistics in RL

   6.3 Swarms on manifolds and directional statistics for unsupervised ML

   6.4 Statistical models for the latent space

   6.5 Kuramoto models for learning (coupled) actions of Lie groups

   6.6 Grassmannian shallow and deep learning

   6.7 Ensembles of coupled oscillators in ML: Beyond Kuramoto models

7. Examples

   7.1 Wahba’s problem

   7.2 Linked robot’s arm (planar rotations)

   7.3 Linked robot’s arm (spatial rotations)

   7.4 Embedding multilayer complex networks (Learning coupled actions of Lorentz groups)

8. Conclusion and References

6.4 Statistical models for the latent space

ariational autoencoders (VAE) are among the most prominent classes of probabilistic graphical models in DL. VAE consists of two NN’s and the latent space. The first network (encoder) embeds input vectors from a high-dimensional vector space X into a lower-dimensional latent space Z; the second network (decoder) maps Z into a vector space Y of the output data. Encoder and decoder networks are trained simultaneously, with the objective of maximizing the likelihood of the observed data x ∈ X by learning over a parametrized probability distributions p(x|θ) in Z. In brief, architecture of VAE can be illustrated by the following simple diagram:

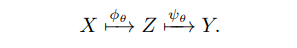
Here, φθ and ψθ denote the maps that are usually implemented through NN’s.

The encoder network learns probabilistic representations of input vectors from X. Once the training is completed, this network becomes unnecessary, and the new data is generated by sampling from a chosen probability distribution p(x|θ) ∈ Z and mapping the samples to Y via the decoder ψθ.

An essential issue in designing VAE is the structure of the latent space. In principle, any family of probability distributions (statistical manifold) can be chosen to model the input data. However, statistical manifolds are not equally convenient for learning algorithms. First, VAE generates the new data through sampling from p(x|θ). This imposes an obstacle for the training, because sampling is not a differentiable operation and one can not backpropagate through this operation. Second, VAE is trained in order to minimize the reconstruction error between the output and input data. This objective is achieved by simultaneous maximization of the log-likelihood of the observed data and minimization of the K-L divergence between the approximate posterior pθ(·|x) and the exact posterior qθ(·|x). This is achieved through the maximization of the evidence lower bound (ELBO). Hence, reasonably simple expression for the K-L divergence is essential for the efficient training.

The second advantage of the Gaussian family is property (P2). A simple expression for the K-L divergence facilitates maximization of ELBO.

In whole, VAE’s with the Gaussian latent space (named normal, or Gaussian, VAE and denoted by N -VAE) are standard and the most popular model. Following the seminal papers [120, 121] on VAE several alternative versions of VAE have been proposed and attracted a lot of interest. One alternative are VAE’s with the latent space consisting of the family of categorical distributions (i.e. distributions over a finite set of outcomes). It has been argued that such an architecture named categorical VAE (we use an abbreviation CAT -VAE) can be advantageous in many setups. The problem of backpropagation through the sampling is circumvented using the "Gumbel-softmax" trick [122]. This trick is based on the fact that categorical distributions can be approximated with the family of absolutely-continuous Gumbel distributions by gradually annealing the "temperature" parameter. Hence, training of CAT -VAE is based on the backpropagation through the family of Gumbel distributions and annealing the temperature in order to approximate the targeted categorical distribution. Maximization of ELBO in CAT -VAE is not difficult, since there is a simple explicit expression for the K-L divergence between two categorical distributions.

Further experiments explored VAE architectures with von Mises-Fisher distributions in the latent space [123, 124]. These architectures have been named spherical VAE and denoted S-VAE. We prefer the abbreviation VMF-VAE in order to emphasize that they assume the von Mises-Fisher family. A difficulty in training VMF-VAE is the backpropagation through the sampling. The reparametrization trick is realized through the rejection-acceptance sampling [125]. It has been argued that VMF-VAE is able to capture directional data [124], or word embeddings [123], where N -VAE fails.

Recently, new VAE architectures with latent dynamics described by continuous-time dynamical systems have been investigated on sequential data (irregular time series) [126, 127]. This idea can be naturally extended to VAE’s with spherical (or toroidal) latent space. Learning of the (sequential) data representations in the latent space can naturally be implemented through the training of the Kuramoto networks. As explained above, in such a way we can implement learning over families vMF, sphC and wC. In conclusion, VAE architectures with wrapped and spherical Cauchy distributions (along with learning embeddings into the latent space by training Kuramoto models) seem like a very promising idea, but is still to be implemented and tested on real-life problems.