Table of Links
-
Experiments
6.2. Discussion on Structural Entropy
Parameter Sensitivity We examine the parameter sensitivity on the dimension of structural entropy in LSEnet, i.e., the height of the partitioning tree H. The clustering results in Table 1 is given by H = 3. Here, we vary the height H in {2, 3, 4, 5}, and report the results on Cora, Citeseer, AMAP and Computer datasets in Fig. 3. It shows that
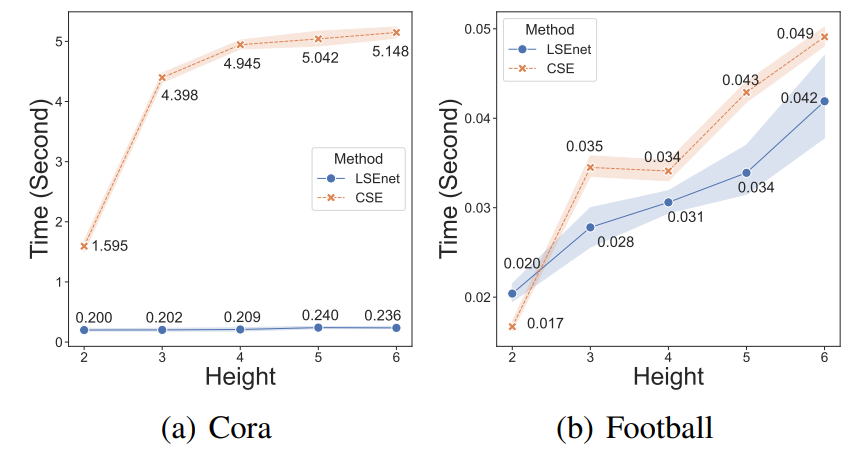
LSEnet generally receives performance gain when increasing the height. Also, LSEnet is able to obtain satisfactory results with small heights.

Embedding Expressiveness. In addition to the cluster assignment, LSEnet learns node embeddings in hyperbolic space. We evaluate the embedding expressiveness regarding link prediction. We compare with the popular GCN (Kipf & Welling, 2017), SAGE (Hamilton et al., 2017) and GAT (Velickovic et al., 2018) in Euclidean space, hyperbolic models including HGCN (Chami et al., 2019) and LGCN
(Zhang et al., 2021), and a recent QGCN in ultra hyperbolic space (Xiong et al., 2022). Results in terms of AUC are provided in Table 3, where we set H as 3 for LSEnet. It shows that hyperbolic embeddings of LSEnet encode the structural information for link prediction.

Authors:
(1) Li Sun, North China Electric Power University, Beijing 102206, China ([email protected]);
(2) Zhenhao Huang, North China Electric Power University, Beijing 102206, China;
(3) Hao Peng, Beihang University, Beijing 100191, China;
(4) Yujie Wang, North China Electric Power University, Beijing 102206, China;
(5) Chunyang Liu, Didi Chuxing, Beijing, China;
(6) Philip S. Yu, University of Illinois at Chicago, IL, USA.
This paper is

